DCF77 Frequenzstandard: Unterschied zwischen den Versionen
imported>Apo |
imported>Apo |
||
| (23 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Als Antenne wird eine herkömmliche Ferritkern-Antenne, wie sie in Funkuhren zu finden ist, verwendet. | Als Antenne wird eine herkömmliche Ferritkern-Antenne, wie sie in Funkuhren zu finden ist, verwendet. | ||
Das empfangene Signal wird durch einen Bandpass auf den 77.5 kHz-Träger reduziert | Das empfangene Signal wird durch einen Bandpass auf den 77.5 kHz-Träger reduziert. | ||
Ein STM32-Microcontroller, dessen | Ein STM32-Microcontroller, dessen PLL von den VCXO gespeist wird, zählt bestimmt die Phasenverschiebung | ||
gegenüber dem DCF77 Signal und korrigiert die Kontrollspannung des VCXO so, dass | |||
die Abweichung auf 0 gemittelt wird. | die Abweichung auf 0 gemittelt wird. | ||
= Signalempfang = | = Signalempfang = | ||
Zum Empfang des Signals wird eine Ferritkern-Antenne verwendet, die aus einem alten Funkwecker entfernt werden kann. | |||
Bei Bedarf kann ein größerer Ferritstab gekauft werden (eBay oder Aliexpress haben 200x10 mm Stäbe für etwa 8 Euro | |||
bzw. 7 USD). Solche Antennen sind recht schmalbandig, was hier von Vorteil ist, und haben im Vergleich zur Wellenlänge | |||
des Signals sehr kleine Dimensionen - eine Welle eines 77.5 kHz Signals hat eine Länge von etwa vier Kilometern. | |||
= Signalaufbereitung = | = Signalaufbereitung = | ||
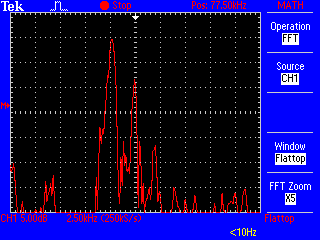
[[Datei:DCF77-Spektrum.png| | [[Datei:DCF77-Spektrum-mit-PC.png|320px|thumb|right|Spektrum an einer Ferritkern-Antenne, störender Einfluss durch die Verbindung vom PC an das Oszilloskop durch einen USB-RS232-Adapter]] | ||
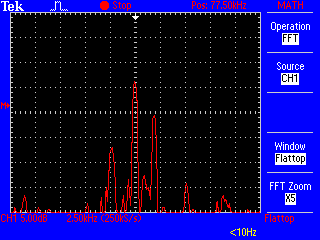
[[Datei:DCF77-Spektrum-ohne-PC.png|320px|thumb|right|Spektrum an einer Ferritkern-Antenne, ohne direkte Verbindung mit dem PC]] | |||
Im Test ist knapp unterhalb der Trägerwelle ein Störsignal zu sehen, das sich in der Regel zwischen 70 und 75 kHz aufhält, aber teilweise | Im Test ist knapp unterhalb der Trägerwelle ein Störsignal zu sehen, das sich in der Regel zwischen 70 und 75 kHz aufhält, aber teilweise | ||
auch näher an die Trägerwelle herankommt. | auch näher an die Trägerwelle herankommt. Dies kommt von dem Rechner, der in der Nähe des Oszilloskops steht. Die Antenne sollte also möglichst weit | ||
von PCs (oder anderen Geräten mit Schaltnetzteilen) aufgebaut und ihr Signal nach Verstärkung über ein abgeschirmtes Kabel zum digitalen Teil | |||
der Schaltung geleitet werden. | |||
Als Filter bietet sich ein Quarzfilter an. Quarzfilter haben eine sehr niedrige Bandbreite, was den Empfang von Sekundenpulsen ungenauer macht. Da | |||
für unseren Zweck die Zeit egal und nur die Trägerwelle von Interesse ist, ist dies belanglos. | |||
Nach dem Filter sollte eine Verstärkung des Signals erfolgen, die eventuell einen AGC (Automatic gain control) Kreis beinhaltet. | |||
* JFET-Buffer (TL084?) | |||
* Quarzfilter als Bandpass um 77.5 kHz | |||
* Verstärkung mit AGC? | |||
== Quarzfilter == | |||
Es wurden 100 77.5 kHz Quarze von [https://www.aliexpress.com/item/77-5KHZ-77-500KHZ-3-8-308-2Pin-DIP-XTAL-Crystal-Oscillator-x-50PCS/1988635809.html AliExpress] bestellt. | |||
In Messungen mit einem [http://sdr-kits.net/VNWA3_Description.html VNWA3] hatten vier davon eine durchschnittliche Serienresonanzfrequenz <math>f_s</math> = 77495.2 Hz, eine Parallelresonanzfrequenz <math>f_p</math> = 77537.5 Hz, und eine Serienkapazität <math>C_s</math> = 1.42187 fF. Mit diesen Werten lässt sich nach [http://www.giangrandi.ch/electronics/crystalfilters/xtalladder.html Iacopo Giangrandis Kristallfilter-Rechner] mit einigen 18 pF (nach Rundung, vorher 16.7 pF und 19.4 pF) Kondensatoren ein Filter bauen, der eine Bandbreite von 8 Hz hat und nach 200 Hz eine Dämpfung von 86 dB erreicht. | |||
= Kontrollalgorithmus = | = Kontrollalgorithmus = | ||
Der Träger wird mit 10 kHz abgetastet, es wird also eine <math>(77.5 % 10) \text{kHz} = 7.5 \text{kHz}</math> Schwingung gemessen. Zu jedem | |||
Zeitschritt wird der Messwert durch Multiplikation mit | |||
<math>\exp(2\pi i\cdot 2500 \text{ Hz }\cdot t)</math> mit 2500 Hz gemischt. Dies entspricht abwechselnder Multiplikation mit | |||
(0,1), (1,0), (0,-1), (-1,0). Die Komponenten der komplexen Zahl werden (wenn sie nicht gerade mit 0 multipliziert wurden) über längere Zeit gemittelt. | |||
Aus den Komponenten lässt sich eine Phase berechnen, und aus deren Ableitung die Frequenzabweichung des Ofenquarzes, die man auf 0 regelt. | |||
Alternativ lässt sich entweder die Phase auf 0 regeln, oder man lässt die Phasenberechnung komplett aus und stellt den Sollpunkt des Reglers z.B. | |||
so ein, dass die In-Phase und Quadratur Komponenten des Vektors gleich sind. Dies kann aber zu Problemen führen, wenn die Frequenz nicht ausreichend | |||
schnell geregelt werden kann und es Phasenüberläufe gibt. | |||
[[Kategorie:Projekte]] | [[Kategorie:Projekte]] | ||
Aktuelle Version vom 12. August 2017, 23:11 Uhr
Ein 10-MHz Quarz (VCXO) wird durch einen STM32 an die Trägerfrequenz des DCF77 Zeitzeichensenders gebunden. Da diese selber an die Atomuhren in Braunschweig gebunden ist und eine relative Standardabweichung von 10^-12 hat, sollte so (bei vorhandenem Signal) ein sehr genaues aber gleichzeitig günstiges Frequenznormal entstehen.
Überblick
Als Antenne wird eine herkömmliche Ferritkern-Antenne, wie sie in Funkuhren zu finden ist, verwendet.
Das empfangene Signal wird durch einen Bandpass auf den 77.5 kHz-Träger reduziert.
Ein STM32-Microcontroller, dessen PLL von den VCXO gespeist wird, zählt bestimmt die Phasenverschiebung gegenüber dem DCF77 Signal und korrigiert die Kontrollspannung des VCXO so, dass die Abweichung auf 0 gemittelt wird.
Signalempfang
Zum Empfang des Signals wird eine Ferritkern-Antenne verwendet, die aus einem alten Funkwecker entfernt werden kann. Bei Bedarf kann ein größerer Ferritstab gekauft werden (eBay oder Aliexpress haben 200x10 mm Stäbe für etwa 8 Euro bzw. 7 USD). Solche Antennen sind recht schmalbandig, was hier von Vorteil ist, und haben im Vergleich zur Wellenlänge des Signals sehr kleine Dimensionen - eine Welle eines 77.5 kHz Signals hat eine Länge von etwa vier Kilometern.
Signalaufbereitung
Im Test ist knapp unterhalb der Trägerwelle ein Störsignal zu sehen, das sich in der Regel zwischen 70 und 75 kHz aufhält, aber teilweise auch näher an die Trägerwelle herankommt. Dies kommt von dem Rechner, der in der Nähe des Oszilloskops steht. Die Antenne sollte also möglichst weit von PCs (oder anderen Geräten mit Schaltnetzteilen) aufgebaut und ihr Signal nach Verstärkung über ein abgeschirmtes Kabel zum digitalen Teil der Schaltung geleitet werden.
Als Filter bietet sich ein Quarzfilter an. Quarzfilter haben eine sehr niedrige Bandbreite, was den Empfang von Sekundenpulsen ungenauer macht. Da für unseren Zweck die Zeit egal und nur die Trägerwelle von Interesse ist, ist dies belanglos.
Nach dem Filter sollte eine Verstärkung des Signals erfolgen, die eventuell einen AGC (Automatic gain control) Kreis beinhaltet.
- JFET-Buffer (TL084?)
- Quarzfilter als Bandpass um 77.5 kHz
- Verstärkung mit AGC?
Quarzfilter
Es wurden 100 77.5 kHz Quarze von AliExpress bestellt. In Messungen mit einem VNWA3 hatten vier davon eine durchschnittliche Serienresonanzfrequenz <math>f_s</math> = 77495.2 Hz, eine Parallelresonanzfrequenz <math>f_p</math> = 77537.5 Hz, und eine Serienkapazität <math>C_s</math> = 1.42187 fF. Mit diesen Werten lässt sich nach Iacopo Giangrandis Kristallfilter-Rechner mit einigen 18 pF (nach Rundung, vorher 16.7 pF und 19.4 pF) Kondensatoren ein Filter bauen, der eine Bandbreite von 8 Hz hat und nach 200 Hz eine Dämpfung von 86 dB erreicht.
Kontrollalgorithmus
Der Träger wird mit 10 kHz abgetastet, es wird also eine <math>(77.5 % 10) \text{kHz} = 7.5 \text{kHz}</math> Schwingung gemessen. Zu jedem Zeitschritt wird der Messwert durch Multiplikation mit <math>\exp(2\pi i\cdot 2500 \text{ Hz }\cdot t)</math> mit 2500 Hz gemischt. Dies entspricht abwechselnder Multiplikation mit (0,1), (1,0), (0,-1), (-1,0). Die Komponenten der komplexen Zahl werden (wenn sie nicht gerade mit 0 multipliziert wurden) über längere Zeit gemittelt.
Aus den Komponenten lässt sich eine Phase berechnen, und aus deren Ableitung die Frequenzabweichung des Ofenquarzes, die man auf 0 regelt. Alternativ lässt sich entweder die Phase auf 0 regeln, oder man lässt die Phasenberechnung komplett aus und stellt den Sollpunkt des Reglers z.B. so ein, dass die In-Phase und Quadratur Komponenten des Vektors gleich sind. Dies kann aber zu Problemen führen, wenn die Frequenz nicht ausreichend schnell geregelt werden kann und es Phasenüberläufe gibt.